Kill the Killer-Sudoku problem
数独的种类有很多,其中一种叫做杀手数独(Killer Sudoku),它是标准数独与数总和数独(Kakuro)的结合,规则如下:
- 基本规则:适用标准数独规则,即每行、每列及每宫(3×3 区域)内填入数字 1~9,且不重复。
- 笼子规则:全盘被虚线框(笼子)划分,每个笼子左上角标有提示数字,表示该框内所有数字之和;同一笼子内数字不能重复。
- 初始状态:通常无预先填好的数字,需通过笼子提示及标准数独规则推理填数。
人类解决杀手数独的技巧
人类解决杀手数独的方法与解决标准数独的方法相似,常见的技巧如下:
注
为简洁,用 x[y] 表示包含 y 格,所有数字之和为 x 的笼子。
- 45 法则:一行/列/宫 9 格之和必为 45,用已知的笼和反推剩余格。
- 举例:某宫 8 格已落入三个笼,和为 38 → 45-38=7,剩下那格必为 7 。
- 固定组合:笼内不可重复,因此某些“笼和+格数”只有唯一或极少的数字组合。
- 举例:笼 4[2] 只能是 {1,3};笼 16[2] 只能是 {7,9} 。
- 组合互斥:两个笼相邻且共用行/列/宫时,唯一可行的组合可能互相“挤掉”冲突数字。
- 举例:笼 5[2] 与 笼 7[2] 共用一列 → 7[2] 不能取 {3,4},否则 5[2] 无法满足 。
- 余数唯一:某格在笼内、行、列、宫三重限制下只剩一个候选数。
- 举例:笼 17[2] 已知可选 {8,9},该行已有 9 → 此格必为 8。
- 隐性数对/三数:在某行/列/宫或笼内,两个(或三个)数字只出现在同一格位,可删除其余候选。
- 举例:笼 10[4] 中数字 1,2 只出现在两格 → 这两格排除 3,4,其余格排除 1,2 。
- 区块删减:某数字在行/列/宫或笼内仅出现在同一区块,则可从该区块外删除该数字。
- 举例:数字 6 在某笼三格中全部位于宫的上半区 → 宫下半区其余格不含 6 。
- 内外扩展 45:把 45 法则扩展到两行、两列或整个盘面,用“溢出”求外部格。
- 举例:第 1~3 列总和 135,笼总和 151 → 151-135=16,说明跨出这三列的两格和为 16,只能是 7+9 。
- 唯一性致命模式:防止出现镜像双解,从而强制某格取某个值。
- 举例:两个 5[2] 笼对称,若都取相同组合会形成致命模式 → 必须一取 {1,4}、另一取 {2,3} 。
- 高低和夹逼:笼和极小或极大时,数字范围天然受限,可迅速定位。
- 举例:笼 6[3] 只能是 {1,2,3},若其中一格已在行内出现 3 → 其余两格只能是 1,2 且顺序可定。
- 交叉排除:把标准数独的行列宫排除法与笼的范围同时应用,交叉过滤候选。
- 举例:笼 22[3] 必含 9;该 9 又必须落在当前行的第 2 宫 → 第 2 宫其余笼不再含 9 。
由于杀手数独初始盘面没有数字,因此需要从一些较小的笼子着手,利用固定组合或内外扩展 45 法则进行启发式搜索。在反复叠加使用上述技巧的情况下,绝大多数杀手数独都能在不靠猜测的情况下稳步推进。
杀手数独的难度比标准数独高出不少(读者可自行尝试)。对人类来说如此,但对计算机呢?计算机解决标准数独的标准方法是回溯法,那么这能否也被用来解决杀手数独呢?
回溯法——本质是暴力搜索
回溯法(Backtracking)可以一句话概括为:用递归方式实现的、带剪枝的深度优先暴力搜索。
相信读者在推进包含许多选项的剧情类游戏(如视觉小说)时,往往会选择先在一条分支路径上走到结局,然后返回存档点换一条新分支路径后再次向前推进,走到该路径的结局。如此循环直至达到最完美的某一个结局(True End)或者满足全结局的收集欲望。而这正是回溯法的基本思想。
将以上思想进行抽象总结:
- 把解空间视为一棵隐式树,用深度优先搜索(DFS)逐枝枚举;一旦发现当前枝不可能产生解,立即“回溯”到上一层,换枝继续枚举。
- 把握三个关键点:
- 路径:当前已经做出的选择(部分解)。
- 选择列表:当前能做的合法选择。
- 结束条件:已构成完整解或无可行选择。
回溯法的核心代码骨架:
def backtrack(path, choices):
if 满足结束条件:
记录解
return
for c in choices:
if 剪枝条件 (c): continue
做出选择
backtrack(path+[c], 新 choices)
撤销选择 # 回溯从代码中可以看出,回溯法的时间复杂度最坏是指数级的。因此剪枝是非常有必要且十分有效的优化策略,枚举量减得越多,耗时也就越少。一些经典的剪枝方法有:
- 约束剪枝:利用题目显式规则提前剔除非法枝(如数独行列宫冲突)。
- 限界剪枝:利用上下界估计剪掉不可能更优的枝(如背包价值上限提前计算)。
- 对称/重复剪枝:利用对称性或记忆化避免重复子树(如八皇后镜像摆放)。
- 顺序优化:把高剪枝效率的决策提前,减少深层无效递归。
即便能通过剪枝减少枚举量,回溯法作为暴力搜索方法,时间开销仍然是巨大的。所以在有更低时间复杂度的高阶算法时通常不会采用回溯法。反过来说,采用回溯法解决的问题通常都是排列/划分/棋盘等没有高阶算法的穷举问题。
利用回溯法解决杀手数独
数独正是利用回溯法解决的典型问题,标准数独如此,杀手数独同样如此。
核心逻辑
分析杀手数独的规则,回溯法思想的三个关键点可以被具体描述为:
- 路径:当前已经填好的数字。
- 选择列表:1~9。
- 结束条件:所有格子都填上数字且满足约束条件。(假设杀手数独总是有解)
按照上面的思路,杀手数独的约束条件只在所有格子都填满时才会进行验证,这会大大增加回溯耗时。因此杀手数独问题需要在约束条件上进行剪枝优化:
- 检查行/列/宫内是否有重复数字。(与标准数独相同)
- 检查笼子内是否有重复数字。
- 若笼子被填满,检查笼子内数字的和是否与标注和相等。
除此之外,由于杀手数独给出的数字和可以视作某种界限,还能利用限界剪枝进一步优化:
- 检查笼子内剩余格子数 N 和当前已填数字之和 S,若 S+1N 大于标注和(剩余格子全部填 1 都会超过标注和),或者 S+9N 小于标注和(剩余格子全部填 9 都达不到标注和),则对该路径剪枝。
以下用 Python 代码展示了核心的回溯逻辑实现(省略了状态变量的定义)。
def backtrack(row, col):
if row == 9:
return True # 所有格子已填满,找到解
next_row = row + (col + 1) // 9
next_col = (col + 1) % 9
if self.board[row][col] != 0:
return backtrack(next_row, next_col) # 跳过已填格子
cage_id = self.cage_index[row][col]
box_idx = (row // 3) * 3 + col // 3 # 计算九宫格索引
for num in range(1, 10):
# 检查行、列、九宫格是否冲突
if self.row_used[row][num] or self.col_used[col][num] or self.box_used[box_idx][num]:
continue
# 检查笼子内数字是否重复
if self.cage_digits[cage_id][num]:
continue
# 备份当前笼子状态
old_current = self.cage_current[cage_id]
old_remaining = self.cage_remaining[cage_id]
# 更新笼子状态
self.cage_current[cage_id] += num
self.cage_remaining[cage_id] -= 1
self.cage_digits[cage_id][num] = True
# 检查笼子约束
current_sum = self.cage_current[cage_id]
rem = self.cage_remaining[cage_id]
total_needed = self.cage_total[cage_id]
valid_cage = True
if current_sum > total_needed:
valid_cage = False
elif rem == 0:
if current_sum != total_needed:
valid_cage = False
else:
if current_sum + rem * 1 > total_needed: # 最小可能值超出
valid_cage = False
elif current_sum + rem * 9 < total_needed: # 最大可能值不足
valid_cage = False
if valid_cage:
# 放置数字并更新标记
self.board[row][col] = num
self.row_used[row][num] = True
self.col_used[col][num] = True
self.box_used[box_idx][num] = True
# 递归填下一个格子
if backtrack(next_row, next_col):
return True
# 回溯:恢复标记
self.board[row][col] = 0
self.row_used[row][num] = False
self.col_used[col][num] = False
self.box_used[box_idx][num] = False
# 恢复笼子状态
self.cage_current[cage_id] = old_current
self.cage_remaining[cage_id] = old_remaining
self.cage_digits[cage_id][num] = False
return False其他细节
如何输入这样一个杀手数独?
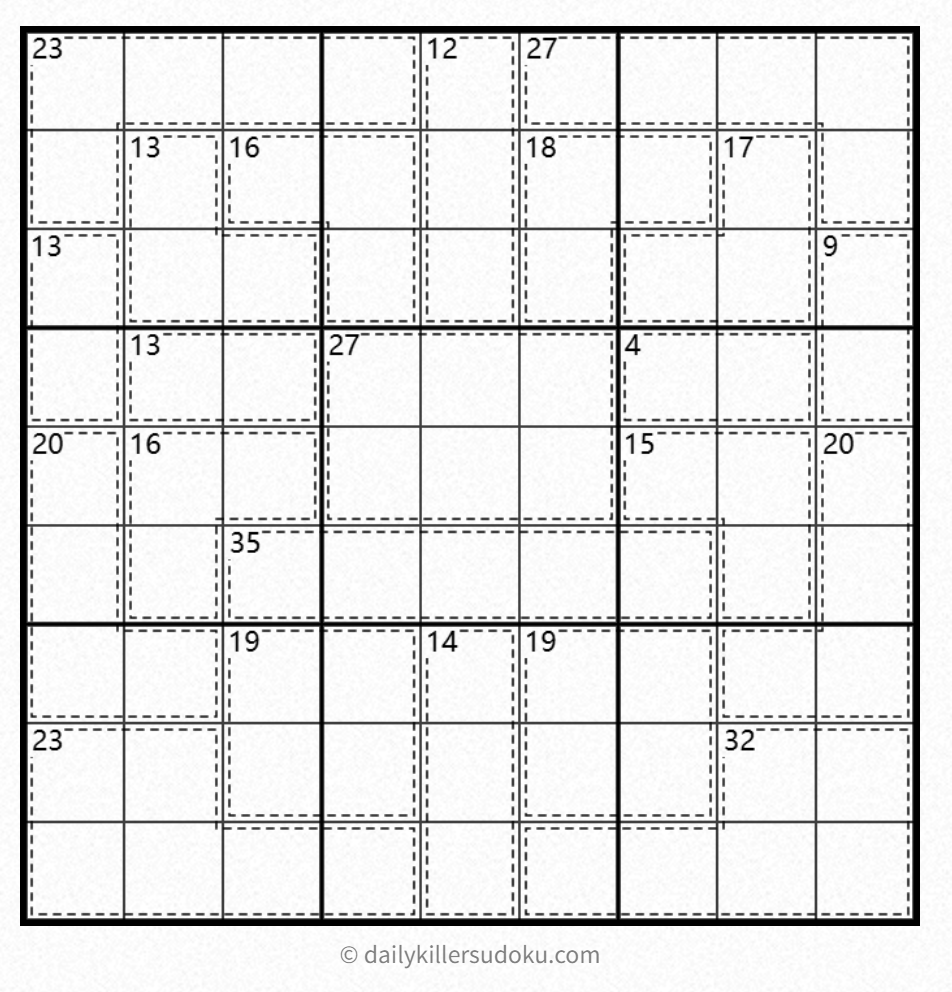
在保持轻量级、不利用 OCR 的情况下,可以对数独盘面进行简单手工编码:将 9×9 的格子从左至右、从上至下用 0~80 进行编码,笼子则用一个元素为元组的数组表示。该元组的第一项是一个数组,记录该笼子中的所有格子;第二项是一个整数,记录该笼子中所有数字之和。
以下展示了文章开头所示 杀手数独盘面 的编码结果。该结果可直接用于输入。
[ ([0,1,2,3,9], 23), ([4,13,22], 12), ([5,6,7,8,17], 27), ([10,19,20], 13), ([11,12,21], 16), ([14,15,23], 18), ([16,24,25], 17), ([18,27], 13), ([26,35], 9), ([28,29], 13), ([30,31,32,39,40,41], 27), ([33,34], 4), ([36,45,54,55], 20), ([37,38,46], 16), ([42,43,52], 15), ([44,53,61,62], 20), ([47,48,49,50,51], 35), ([56,57,65,66], 19), ([58,67,76], 14), ([59,60,68,69], 19), ([63,64,72,73,74,75], 23), ([70,71,77,78,79,80], 32) ]能否直观展示回溯过程?程序运行速度如何?
可以在每次修改盘面数字时覆盖打印盘面以展示每次回溯的状态,这也能更深刻地体会到回溯法本质是暴力搜索的事实——在不断地试错中前进。但是需要注意,可视化回溯过程会大幅降低运行速度。同样的杀手数独问题,在未开启可视化时用时 2 秒解决,但在开启可视化后需要 8384 秒才能解决。
最后放上完整的 Python 代码:
# Made by Wanakachi
import time
import sys
class KillerSudokuSolver:
def __init__(self, cages):
# 初始化棋盘和数据结构
self.board = [[0] * 9 for _ in range(9)]
self.cage_index = [[-1] * 9 for _ in range(9)] # 记录每个格子所属笼子的 ID
self.cages = cages
self.num_cages = len(cages)
self.cage_total = [0] * self.num_cages # 每个笼子的目标和
self.cage_current = [0] * self.num_cages # 每个笼子当前已填数字之和
self.cage_remaining = [0] * self.num_cages # 每个笼子剩余未填格子数
self.cage_digits = [[False] * 10 for _ in range(self.num_cages)] # 记录每个笼子中数字是否已使用
# 初始化行、列、九宫格的数字使用情况
self.row_used = [[False] * 10 for _ in range(9)]
self.col_used = [[False] * 10 for _ in range(9)]
self.box_used = [[False] * 10 for _ in range(9)]
# 根据 cages 输入填充数据结构
for cage_id, (cells, total) in enumerate(cages):
self.cage_total[cage_id] = total
self.cage_remaining[cage_id] = len(cells)
for cell_index in cells:
r = cell_index // 9
c = cell_index % 9
self.cage_index[r][c] = cage_id
# 初始化显示状态
self.last_board = [[' '] * 9 for _ in range(9)]
self.displayed = False
def display_board(self, row=None, col=None, action=""):
"""显示当前棋盘状态"""
if not self.displayed:
# 首次显示,打印完整的棋盘框架
print("\n" + "="*50)
print(f"杀手数独求解器 | 当前操作:{action}")
print("="*50)
# 打印列号
col_header = " "
for c in range(9):
col_header += f" {c+1} " if c % 3 == 2 else f" {c+1} "
print(col_header)
# 打印顶部边框
print(" +" + "---+---+----+" * 3)
self.displayed = True
else:
# 非首次显示,回到棋盘顶部
sys.stdout.write("\033[{}A".format(18)) # 向上移动 18 行
# 打印棋盘内容
for r in range(9):
# 行号
print(f"{r+1} |", end="")
for c in range(9):
# 每 3 列添加分隔线
if c % 3 == 0 and c > 0:
print("|", end="")
# 获取当前格子的值和上次显示的值
cage_id = self.cage_index[r][c]
value = self.board[r][c]
last_value = self.last_board[r][c]
no_number_yet = False
# 确定显示内容和颜色
if r == row and c == col:
# 当前操作的格子
display_value = f"\033[93m{value if value != 0 else '.'}\033[0m" # 黄色
elif value != 0:
# 已填数字的格子
display_value = f"\033[92m{value}\033[0m" # 绿色
else:
# 未填数字的格子
display_value = f"\033[90m{cage_id}\033[0m" if cage_id != -1 else '.' # 灰色
no_number_yet = True
# 只在值变化时更新显示
if str(value) != last_value:
self.last_board[r][c] = str(value) if value != 0 else ' '
# 固定宽度输出
same_width_value = f" {display_value} " if no_number_yet and cage_id > 9 else f" {display_value} "
sys.stdout.write(same_width_value)
else:
# 固定宽度输出
same_width_value = f" {display_value} " if no_number_yet and cage_id > 9 else f" {display_value} "
sys.stdout.write(same_width_value)
print("|")
# 每 3 行添加分隔线
if r % 3 == 2 and r < 8:
print(" +" + "---+---+----+" * 3)
else:
print(" +" + "---+---+----+" * 3)
sys.stdout.flush()
def solve(self, visualization=True):
"""解决杀手数独问题"""
# 开始求解
if visualization:
self.display_board(action="开始求解...")
time.sleep(1)
# 回溯求解函数
def backtrack(row, col):
if row == 9:
if visualization:
self.display_board(action="求解完成!")
return True # 所有格子已填满,找到解
next_row = row + (col + 1) // 9
next_col = (col + 1) % 9
if self.board[row][col] != 0:
return backtrack(next_row, next_col) # 跳过已填格子
cage_id = self.cage_index[row][col]
box_idx = (row // 3) * 3 + col // 3 # 计算九宫格索引
for num in range(1, 10):
if visualization:
self.display_board(row, col, f"尝试 {num}")
# 检查行、列、九宫格是否冲突
if self.row_used[row][num] or self.col_used[col][num] or self.box_used[box_idx][num]:
continue
# 检查笼子内数字是否重复
if self.cage_digits[cage_id][num]:
continue
# 备份当前笼子状态
old_current = self.cage_current[cage_id]
old_remaining = self.cage_remaining[cage_id]
# 更新笼子状态
self.cage_current[cage_id] += num
self.cage_remaining[cage_id] -= 1
self.cage_digits[cage_id][num] = True
# 检查笼子约束
current_sum = self.cage_current[cage_id]
rem = self.cage_remaining[cage_id]
total_needed = self.cage_total[cage_id]
valid_cage = True
if current_sum > total_needed:
valid_cage = False
elif rem == 0:
if current_sum != total_needed:
valid_cage = False
else:
if current_sum + rem * 1 > total_needed: # 最小可能值超出
valid_cage = False
elif current_sum + rem * 9 < total_needed: # 最大可能值不足
valid_cage = False
if valid_cage:
# 放置数字并更新标记
self.board[row][col] = num
self.row_used[row][num] = True
self.col_used[col][num] = True
self.box_used[box_idx][num] = True
if visualization:
self.display_board(row, col, f"放置 {num}")
# 递归填下一个格子
if backtrack(next_row, next_col):
return True
# 回溯:恢复标记
self.board[row][col] = 0
self.row_used[row][num] = False
self.col_used[col][num] = False
self.box_used[box_idx][num] = False
if visualization:
self.display_board(row, col, f"回溯 {num}")
# 恢复笼子状态
self.cage_current[cage_id] = old_current
self.cage_remaining[cage_id] = old_remaining
self.cage_digits[cage_id][num] = False
if visualization:
self.display_board(row, col, "回溯")
return False
# 开始求解
result = backtrack(0, 0)
return self.board if result else None
def print_solution(self):
"""打印最终解决方案"""
print("\n" + "="*50)
print("杀手数独最终解:")
print("="*50)
# 打印列号
col_header = " "
for c in range(9):
col_header += f" {c+1} " if c % 3 == 2 else f" {c+1} "
print(col_header)
# 打印顶部边框
print(" +" + "---+---+----+" * 3)
for r in range(9):
# 行号
print(f"{r+1} |", end="")
for c in range(9):
# 每 3 列添加分隔线
if c % 3 == 0 and c > 0:
print("|", end="")
# 获取当前格子的值
value = self.board[r][c]
display_value = f"\033[92m{value}\033[0m" if value != 0 else '.'
print(f" {display_value} ", end="")
print("|")
# 每 3 行添加分隔线
if r % 3 == 2 and r < 8:
print(" +" + "---+---+----+" * 3)
else:
print(" +" + "---+---+----+" * 3)
print("="*50 + "\n")
# 示例用法
if __name__ == "__main__":
# 示例输入
# 这里定义了三个不同难度的笼子配置
cages_1 = [
([0,1,2], 19),
([3,4,5], 20),
([6,7,16], 11),
([8,17], 7),
([9,10,18,19], 16),
([11,12], 15),
([13,22], 10),
([14,15,23], 14),
([20,21,30], 6),
([24,33], 13),
([25,26], 15),
([27,28,36,45], 17),
([29,38], 11),
([31,32], 11),
([34,43], 10),
([35,44,52,53], 14),
([37,46], 15),
([39,40,41], 14),
([42,51], 12),
([47,56], 9),
([48,49], 15),
([50,59,60], 6),
([54,55], 11),
([57,65,66], 18),
([58,67], 7),
([61,62,70,71], 24),
([63,72], 10),
([64,73,74], 11),
([68,69], 6),
([75,76,77], 20),
([78,79,80], 18)
]
cages_5 = [
([0,1,2,9,18], 20),
([3,4,5,6,13], 27),
([7,16,25,26], 14),
([8,17], 16),
([10,11,12,19,20,28], 31),
([14,15], 8),
([21,29,30], 17),
([22,31], 3),
([23,32], 16),
([24,33], 11),
([27,36,37,45,54], 28),
([34,35,43], 16),
([38,39], 5),
([40,41,49,50], 26),
([42,51,52], 12),
([44,53], 10),
([46,55], 13),
([47,48], 4),
([56,57], 15),
([58,59,68], 10),
([60,61,62,69,70,78], 31),
([63,64,65,74], 20),
([66,67,75], 16),
([71,79,80], 14),
([72,73], 10),
([76,77], 12)
]
cages_10 = [
([0,1,2,3,9], 23),
([4,13,22], 12),
([5,6,7,8,17], 27),
([10,19,20], 13),
([11,12,21], 16),
([14,15,23], 18),
([16,24,25], 17),
([18,27], 13),
([26,35], 9),
([28,29], 13),
([30,31,32,39,40,41], 27),
([33,34], 4),
([36,45,54,55], 20),
([37,38,46], 16),
([42,43,52], 15),
([44,53,61,62], 20),
([47,48,49,50,51], 35),
([56,57,65,66], 19),
([58,67,76], 14),
([59,60,68,69], 19),
([63,64,72,73,74,75], 23),
([70,71,77,78,79,80], 32)
]
solver = KillerSudokuSolver(cages_5)
start_time = time.time()
# 可视化会严重拖慢求解速度(约慢 4000 倍),建议在调试时开启
solution = solver.solve(visualization=False)
end_time = time.time()
if solution:
solver.print_solution()
print(f"求解时间:{end_time - start_time:.4f}秒")
else:
print("未找到解决方案!")